On Reddit, u/spriteguard asks:
Do you have any diagrams of smaller numbers for comparison? I’d love to see a whole sequence of these.
I have work to put off, so I couldn’t resist the challenge. Like the previous post, these are Tromp diagrams showing lambda calculus expressions that evaluate to Church integers.
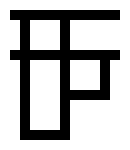
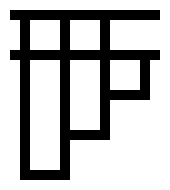
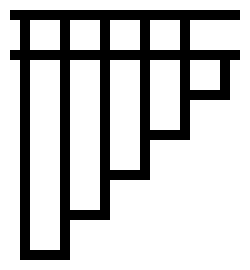
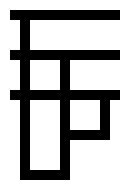
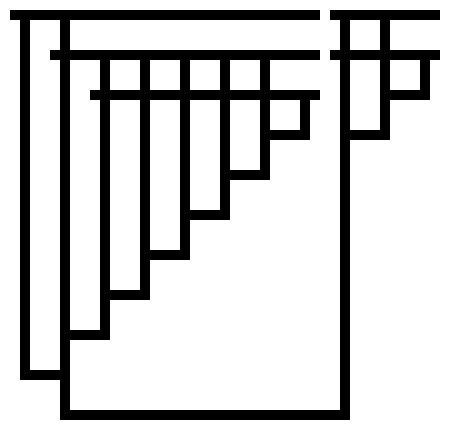
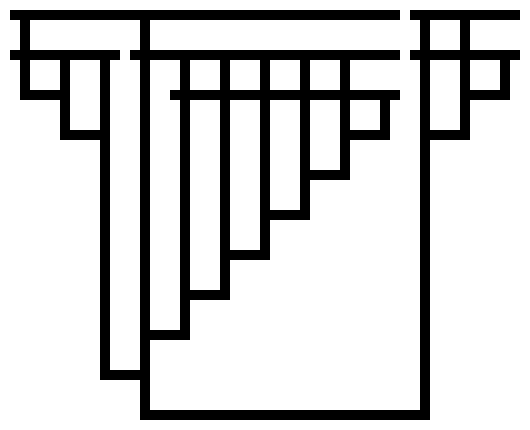
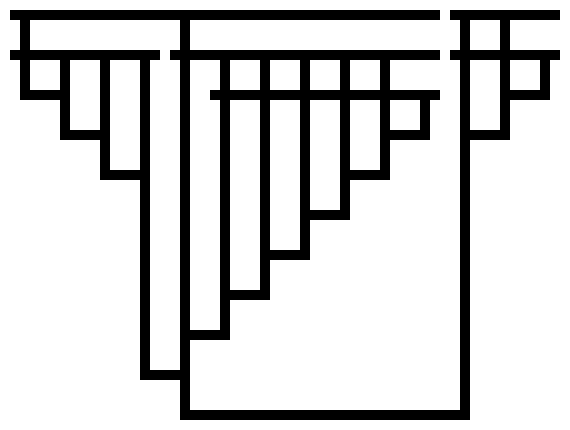
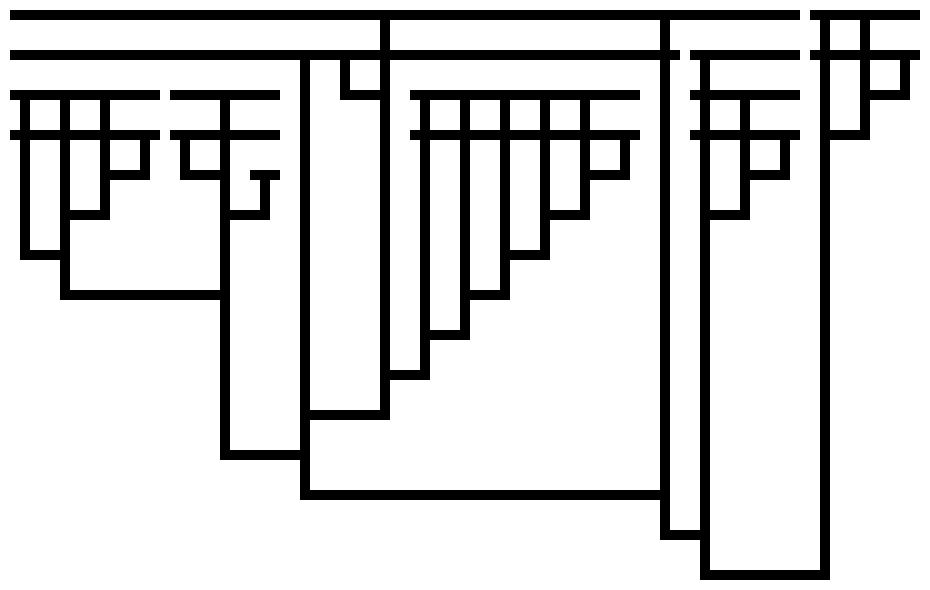
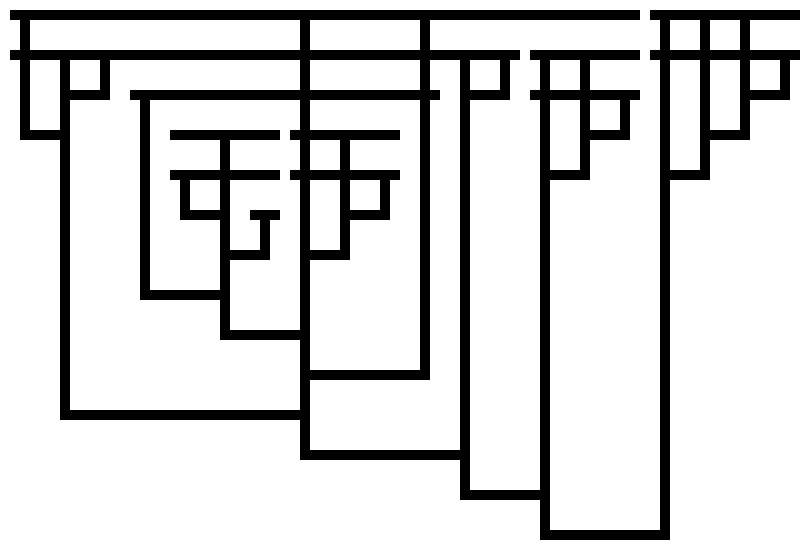
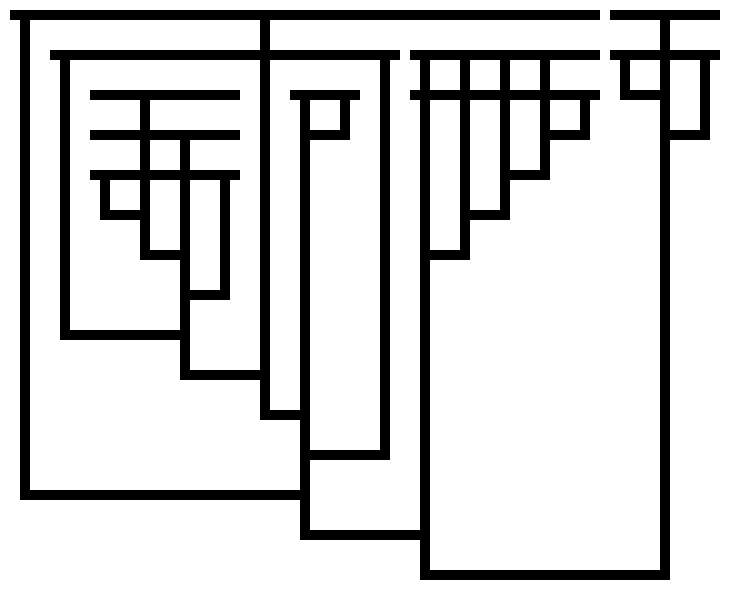
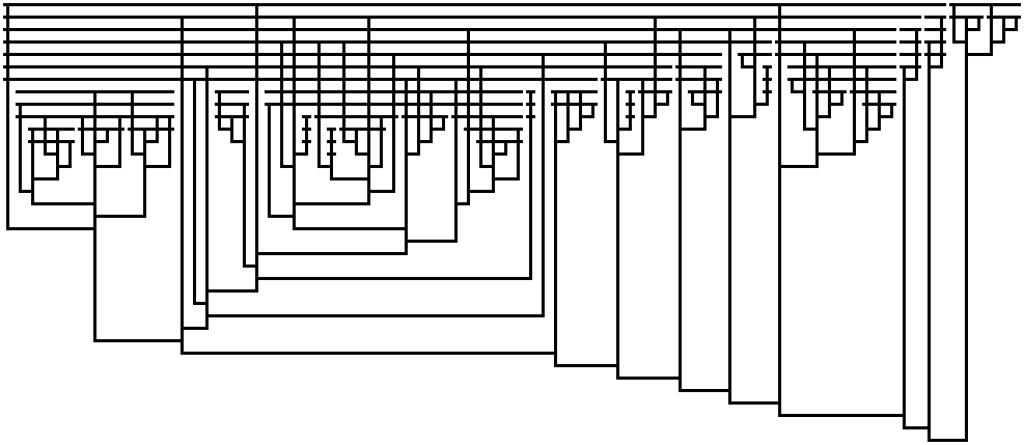
Code to generate these diagrams is on Github; I generated these with the command
./trylambda --outdir /tmp/out demofiles/smallernums.olc demofiles/graham.olc demofiles/fgh.olc demofiles/slow.olc
Minds aren't magic 
how would TREE(3), SCG(13) and Loader’s Number look in a Tromp diagram?
I don’t understand these numbers well enough to implement them myself. I encourage you to download my software and implement them!
Curiously, a diagram for a number exceeding Graham’s monster is no larger than that for the number 10; both take 49 bits.
You can find Loader’s number in blc at https://codegolf.stackexchange.com/questions/176966/golf-a-number-bigger-than-loaders-number/274634#274634
Nice! What’s the 49 bit large number?
Melo’s number [1] is (λj. j j) (λy. y (y (λg λm. m g (λf λx. f (f x))))) or
0100011010000110011000000101101100000011100111010 in blc.
I’d add a diagram, but the imageMagick tool on my outdated Mac is currently broken, and it seems this blog doesn’t support literal code blocks.
[1] https://github.com/tromp/AIT/blob/master/fast_growing_and_conjectures/melo.lam
Must you nerdsnipe me like this when I’m trying to get things done…
what is the formula of your own large number
what is the formula of your own large number f_{ω^ω + 1}(4)
Do you mean the formula in lambda calculus? You can find that here